Zdjęcie z otwartych źródeł W świecie matematyki prawdziwa sensacja. Znaleziono nową różnorodność pięciokątów, które mogą obejmować samolot bez nakładania się i rozrywania. Według naukowców to piętnasty z tych pięciokątów, a także pierwszy otwarty za nimi ostatnie trzy dekady.
Aby objąć samolot, możesz użyć trójkątów i czworokąty o dowolnym kształcie, ale tak jest w przypadku pięciokątów wiele więcej. Samolot nie może być pokryty zwykłymi pięciokątami, ale niektóre nieprawidłowe są odpowiednie do takich celów. Za sto lat, poszukiwanie takich postaci jest jednym z najciekawszych i najbardziej interesujących złożone problemy matematyczne.
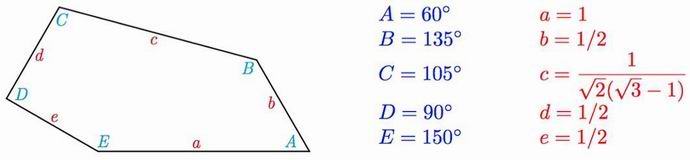Zdjęcie z otwartych źródeł
Wszystko zaczęło się w 1918 roku – wtedy Karlowi Reinhardowi udało się otworzyć pierwsze pięć pasujących pięciokątów. Przez pół wieku wierzono w to matematyk znalazł wszystkie możliwe formy, ale w 1968 r. R.B. Kershner odkrył jeszcze trzy pięciokąty, aw 1975 roku dzięki Richardowi James, ich liczba osiągnęła dziewięć. W ciągu następnych kilku lat zwykła amerykańska gospodyni domowa Marjorie Rice, chętna matematyki i dowiedziałem się o poszukiwaniu takich liczb pięciokątnych, znaleziono jeszcze cztery formy. W końcu Rolf Stein przyniósł numer pięciokąty zdolne do pokrycia samolotu bez przerw, do czternaście w 1985 roku.
Warto zauważyć, że pod tym względem pięciokąty są jedyna postać, która pozostawia miejsce na nowe formy. W 1963 naukowcy udowodnili, że tylko trzy odmiany sześciokąty mogą obejmować samolot. Wśród heptagonów ośmiokąty, devtagony i tak dalej nie ma ogólnie.
Zdjęcie z otwartych źródeł
Przez trzydzieści lat po tym, jak Rolf Stein przyniósł numer pięciokąty do czternastu, nie znaleziono nowych kształtów. I tutaj wprowadzono grupę specjalistów z University of Washington nowy rodzaj pięciokąta. Według naukowców to właśnie je tworzy pomógł znaleźć dokładne wyszukiwanie komputera.
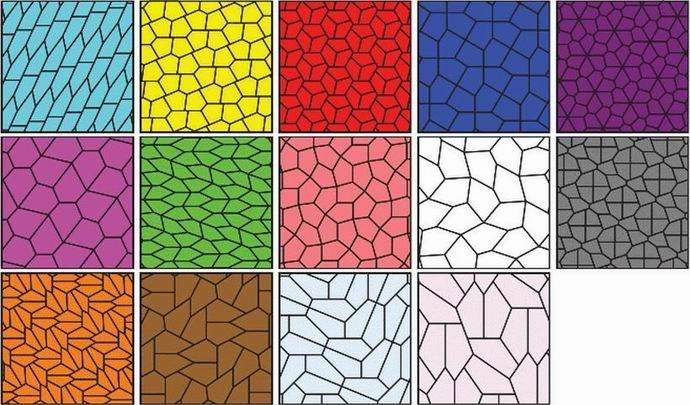
Dla wielu z nas to odkrycie może wydawać się całkowicie abstrakcyjny i bezużyteczny, ale na pewno tak praktyczne zastosowanie. Najbardziej oczywistą opcją jest bez wątpienia jest produkcja płytek.
Zdjęcie z otwartych źródeł
